学习机器学习不可避免的会接触到VC维,它在机器学习领域是一个很基础但很重要的概念,它给机器学习提供了坚实的理论基础。但直到在我写这篇博客之前,我对VC的理解还只停留在它能刻画假设空间的复杂度这样浅显的层次。本文就来理一理VC维(Vapnik–Chervonenkis dimension)的来龙去脉,搞清楚其本质。
1. 可学习的条件
既然说VC维给机器学习提供了坚实的理论基础,那么就有必要来看看机器学习算法可学习的条件是什么。
1.1 学习的过程
一个基本的机器学习过程如图1.1所示(本文图片若无特别说明即来自于台大机器学习基石课程课件,Coursera课程地址)。解释一下下图中的一些概念:$\mathcal{A}$ 表示学习算法,$f$ 表示学习的目标假设(可以是一个函数,也可以是一个分布),$\mathcal{H}$ 表示假设空间,$g$ 表示我们求解的用来预测的假设,$g$ 是属于 $\mathcal{H}$ 的。
机器学习的过程就是:通过算法 $\mathcal{A}$,在假设空间 $\mathcal{H}$ 中,根据训练样本集 $\mathcal{D}$,选择最好的假设作为 $g$ 使 $g$ 近似于 $f$。
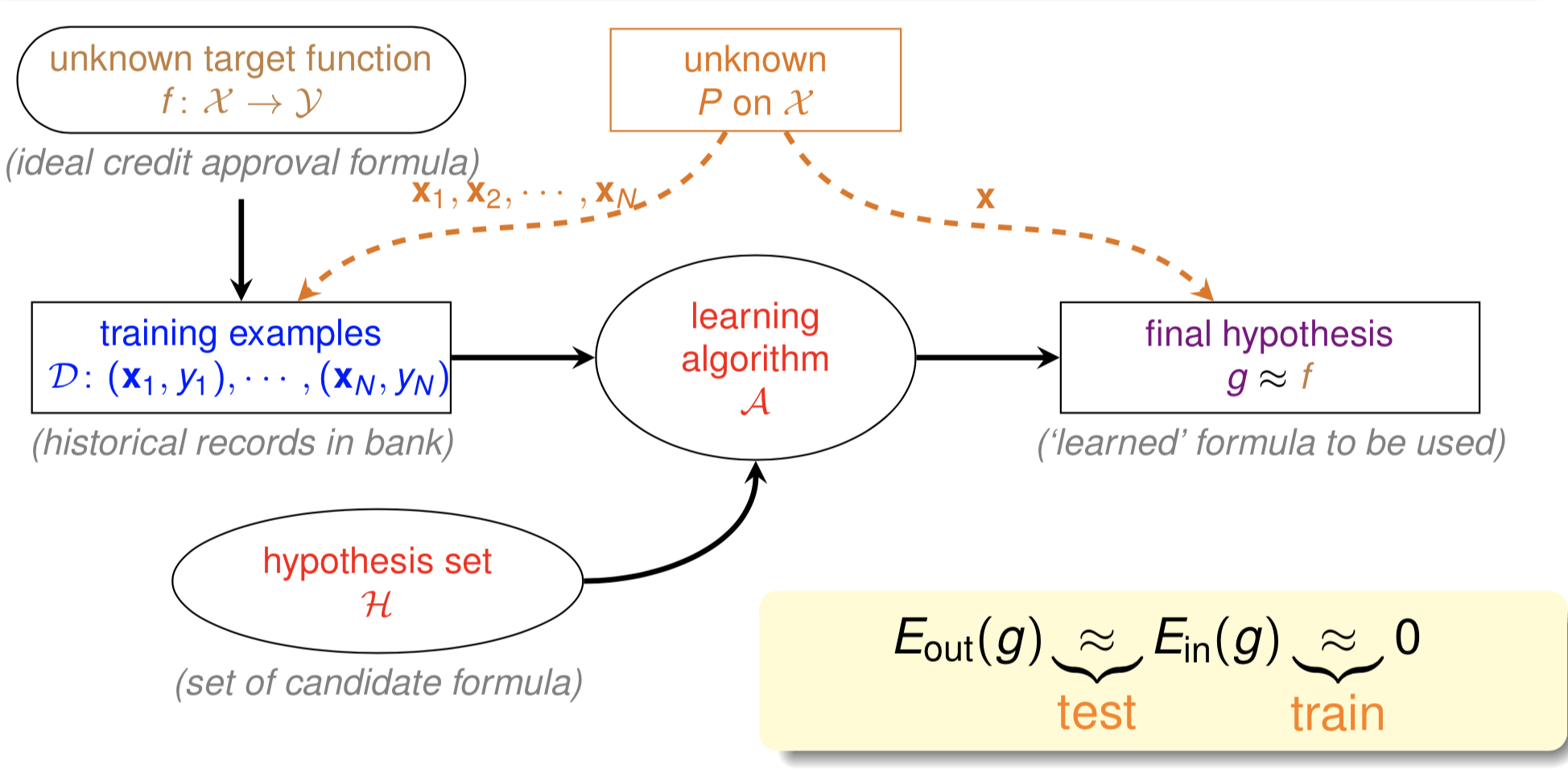
图1.1中的 $E_{out}(g)$ 和 $E_{in}(g)$ 是两个重要的概念:
- $E_{out}(g)$,学到的假设 $g$ 在除了训练样本外的其他所有样本(out-of-sample)上的损失,称为期望误差,也称泛化误差。
- $E_{in}(g)$,学到的假设 $g$ 在训练样本(in-of-sample)上的损失,称为经验误差。
我们的目标是选择最好的假设作为 $g$ 使 $g$ 近似于 $f$,而 $E_{out}(f) = 0$,也即我们的目标是使 $E_{out}(g) \approx 0$。但我们是没法获得训练样本外的其他所有样本的,那也就没法计算 $E_{out}(g)$ 了,这该怎么办呢?
1.2 Hoeffding不等式
在回答1.1最后的问题之前,先来看看Hoeffding不等式。
来看图1.2所述的问题: 设瓶子里的橙色球占比为 $\mu$,从瓶子中随机抽取出N个样本,这N个样本中橙色球占比是 $\nu$。我们可以将 $\mu$ 看作1.1节中的$E_{out}(g)$,将 $\nu$ 看作是 $E_{in}(g)$,我们现在并不知道 $\mu$ 和 $E_{out}(g)$,只知道 $\nu$ 和 $E_{in}(g)$,我们可以从 $\nu$ 推断出关于 $\mu$ 的什么吗?
可以将 $\nu$ 看作是样本期望,$\mu$ 则是总体期望。
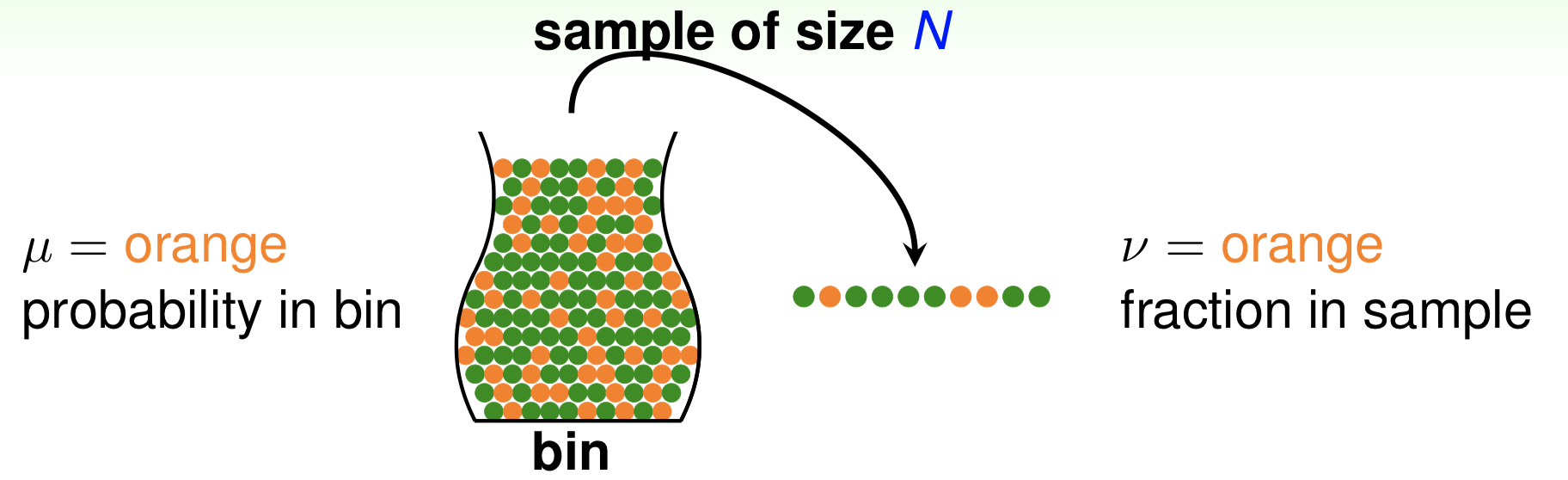
直觉上,如果我们有更多的样本(抽出很多的球),则 $\nu$ 应该越来越接近总体期望 $\mu$。事实上,这里可以用hoeffding不等式表示如下:
$$
\mathbb{P}[|\nu - \mu| > \epsilon] \leq 2 \exp \left(-2 \epsilon^2 N \right) \tag{1.2.1}
$$
从hoeffding不等式可以看出,当N越来越大时,$\nu$ 和 $\mu$ 之差大于 $\epsilon$ 的概率的上界越来越接近0,所以样本期望 $\nu$ 越来越接近总体期望 $\mu$,即 $\nu$ 和 $\mu$ 概率近似相等(probably approximately correct, PAC)了。
1.3 可学习的条件
有了1.2节的铺垫,我们就可以来回答1.1节的问题了。
对于任意固定的假设 $h$,当训练样本量N足够大,类比于1.2节的例子,可以通过样本集上的经验误差 $E_{in}(h)$ 推测总体的期望误差 $E_{out}(h)$。基于hoeffding不等式,我们得到下面式子:
$$
\mathbb{P}[|E_{in}(h) - E_{out}(h)| > \epsilon] \leq 2 \exp(-2 \epsilon^2 N) \tag{1.3.1}
$$
根据上面不等式,我们可以推断,当N足够大时,$E_{in}(h)$ 和 $E_{out}(h)$ 将非常接近。
注意在上面推导中,我们是针对某一个特定的假设 $h$。在我们的假设空间 $\mathcal{H}$ 中,往往有很多个假设(甚至于无穷多个)。那么对于假设空间 $\mathcal{H}$ 中的任意的假设 $h$,$E_{in}(h)$ 和 $E_{out}(h)$ 之差大于 $\epsilon$ 的概率的上界会是什么呢?
发生概率很小的事件在很多次实验中发生概率就会变得很大。例如连续丢5次硬币,事件”五次都是正面朝上”的概率是 $\frac 1 {32}$。但是如果100个人做这个实验,事件”五次都是正面朝上”的发生的概率就是 $1 - ({\frac {31} {32}})^{100} > 0.95$。所以对于特定的假设 $h$,$E_{in}(h)$ 和 $E_{out}(h)$ 很接近,但是对于 $\mathcal{H}$ 中任意的假设这就不一定了。
这里假定 $\mathcal{H}$ 中有 $M$ 个假设 $h_1,h_2,…h_M$,则有如下推导:
$$
\mathbb{P}[\mathbf{E}(h_1)> \epsilon \cup \mathbf{E}(h_2)> \epsilon \space … \cup \mathbf{E}(h_M)> \epsilon] \\
\leq \mathbb{P}[\mathbf{E}(h_1)> \epsilon] + \mathbb{P}[\mathbf{E}(h_2)> \epsilon] \space … + \mathbb{P}[\mathbf{E}(h_M)> \epsilon] \\
\leq 2M\exp(-2 \epsilon^2 N) \tag{1.3.2}
$$
其中 $\mathbf{E}(h_i) = |E_{in}(h_i) - E_{out}(h_i)|$。
根据式 $(1.3.2)$ 知
$$
\forall g \in \mathcal{H}, \mathbb{P}[|E_{in}(g) - E_{out}(g)| > \epsilon] \leq 2M \exp(-2 \epsilon^2 N) \tag{1.3.3}
$$
上面式子的含义就是:在假设空间 $\mathcal{H}$ 中,对于任意一个假设 $g$,$E_{in}(g)$ 和 $E_{out}(g)$ 之差大于 $\epsilon$ 的概率的上界是 $2M \exp(−2 \epsilon^2 N)$。注意这个上界与训练样本数 $N$ 和假设空间假设数 $M$ 密切相关。
本文的所有讨论都是围绕式(1.3.3)进行的!!!
所以,根据式 $(1.3.3)$,我们就知道了可学习的两个核心条件是:
- 学习算法 $\mathcal{A}$ 能够从 $\mathcal{H}$ 选出的假设 $g$ 满足 $E_{in}(g) \approx 0$。再结合条件2即达到了 $E_{out}(g) \approx 0$ 的目标。
- 假设空间 $\mathcal{H}$ 中假设数 $M$ 是有限的且训练样本数 $N$ 足够大。此时可保证式(1.3.3)右边上界趋于0,即学习算法 $\mathcal{A}$ 从 $\mathcal{H}$ 选出的任意假设 $g$ 都满足 $E_{in}(g) \approx E_{out}(g)$。
上面这两个核心条件,也正好对应着train和test这两个过程:
- train过程希望经验误差$E_{in}(g)$ 尽可能小;
- test过程希望在真实环境中的期望误差$E_{out}(g)$也尽可能小,即$E_{out}(g)$接近于$E_{in}(g)$。
所以我们不应该只关心如何利用学习算法找到使 $E_{in}(g)$ 很小的 $g$。因为如果想让学习可行,也要保证$E_{out}(g)$接近于$E_{in}(g)$。
来分析一下 $M$ 的大小对于两个条件的满足情况:
- 当 $M$ 较小时,由式$(1.3.3)$知条件2很容易满足,但是由于可选的 $g$ 的数目 $M$ 较小,所以条件1不容易满足;
- 当 $M$ 较大时,由于可选的 $g$ 的数目 $M$ 较大,所以条件1很容易满足,但是条件2不容易满足。
由此可见,假设数 $M$ 在这两个核心条件中有着重要作用,应该合理选取。但是往往一个假设空间(如二维平面的所有直线)的假设数是很大的甚至是无穷的,此时式$(1.3.3)$中的上界就成了无穷大没有任何约束意义,也即不满足条件2,学习变得不可行,这该怎么办呢?
2. VC维
2.1 有效假设数
在式$(1.3.2)$的推导中,我们用到了这样一个概率不等式:
$$
\mathbb{P}(A_1 \cup A_2 \space … \cup A_M) \leq \sum_{i=1}^M\mathbb{P}(A_i) \tag{2.1.1}
$$
我们知道,当 $A_i$ 相互独立时上式取等号。但事实上,假设空间里的 $h_i$ 之间并不是完全独立的,它们是有很大的重叠的,也就是在 $M$ 个假设中,有很多假设都可以归为同一类。
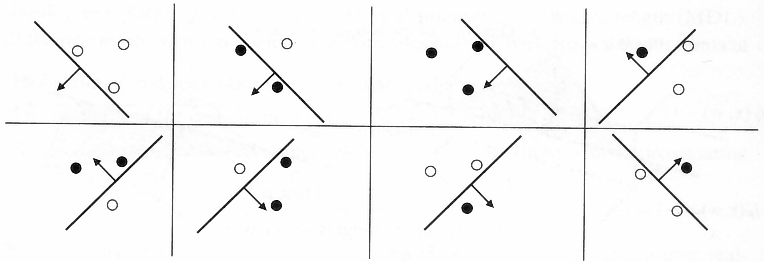
下面用二维假设空间为例解释一下上述重叠性。我们知道二维假设空间的所有假设数(即直线条数)为 $\infty$,但是如图2.1所示,可以将这些假设分为两类,一类是把x1判断为正例,另一类是把x1判断为负例。
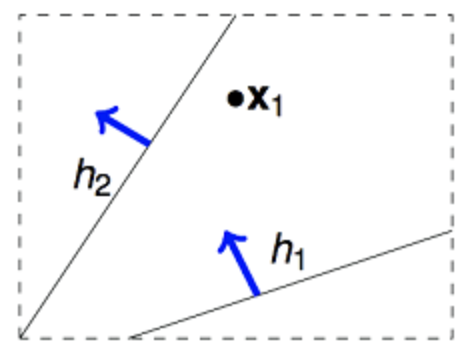
那如果在平面上有两个不同的数据点x1,x2,这样的话,假设空间 $\mathcal{H}$ 中的无数条直线可以分为4类。那依次类推,3个数据点情况下,$\mathcal{H}$ 中最多有8类(当三个点在同一直线上时只有6类)。4个数据点时,$\mathcal{H}$ 中最多有14类(注意不是16类),如下图所示。
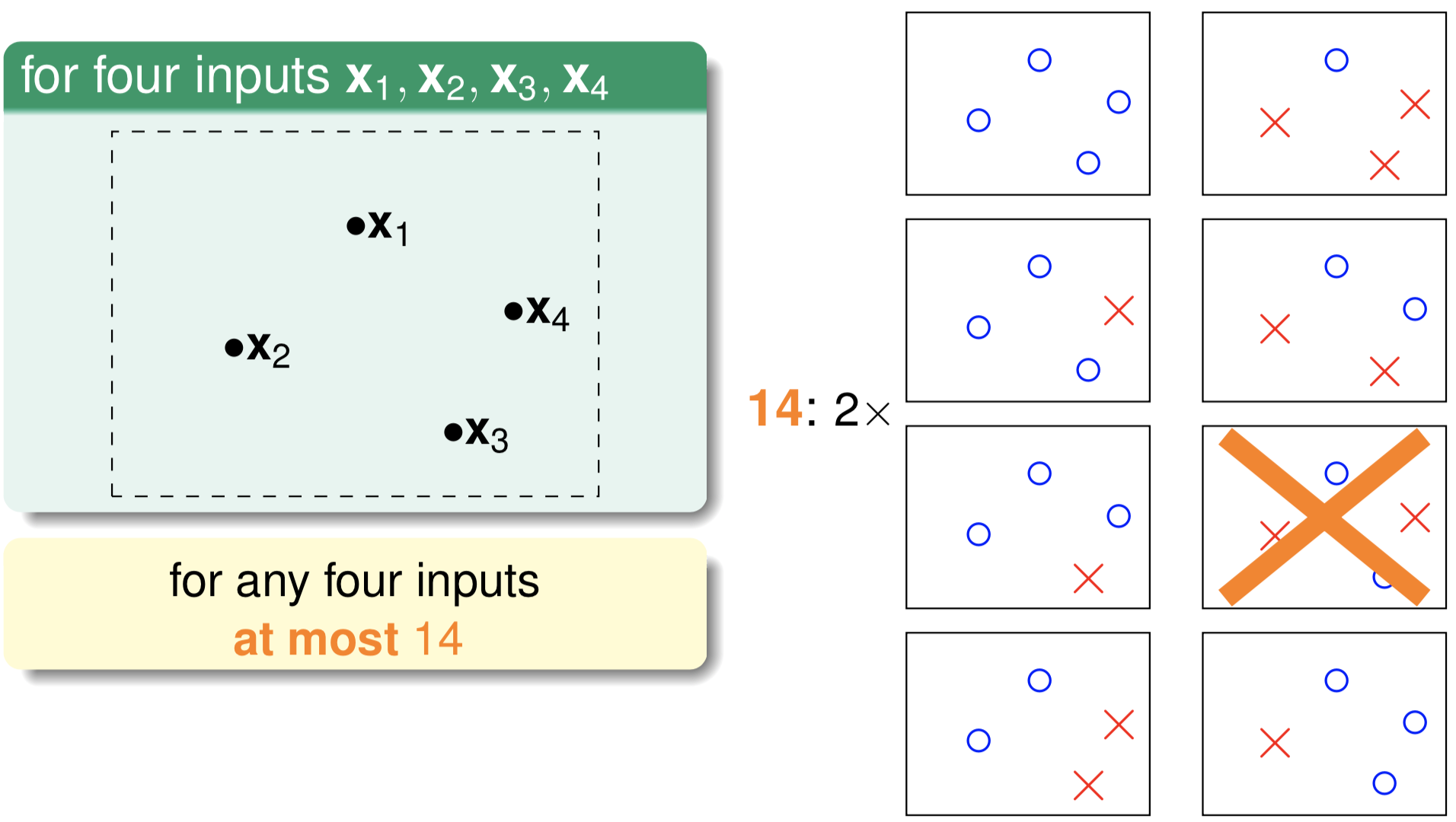
从上面的分析可知,虽然假设空间假设数 $M$ 一般非常大(甚至无穷),但在特定的样本集上,有效的假设数目是有限的,也即式$(1.3.3)$中的 $M$ 是有限的,所以可以重写式$(1.3.3)$如下:
$$
\forall g \in \mathcal{H}, \mathbb{P}[|E_{in}(g) - E_{out}(g)| > \epsilon] \leq 2\cdot \text{effective}(M) \exp(-2 \epsilon^2 N) \tag{2.1.2}
$$
2.2 对分和增长函数
为了探究式$(2.1.2)$中的 $\text{effective}(M)$ ,先引入对分(dichotomy) 的概念:
对于假设空间 $\mathcal{H} = \lbrace h: \mathcal{X} \to \lbrace+1,-1\rbrace \rbrace$,我们称
$$
h(X_1, X_2,…,X_N) = (h(X_1), h(X_2),…,h(X_n)) \in \lbrace+1,-1 \rbrace ^N
$$
为一个对分,即一个对分表示样本的一种标记结果,$\mathcal{H}(X_1, X_2,…,X_N)$ 表示假设空间 $\mathcal{H}$ 在训练集 $\mathcal{D}$ 上的所有对分。
例如,若 $N = 4$且数据为二维时,参见图2.2,有如下表格:
| 假设空间 $\mathcal{H}$ | $\mathcal{H}(X_1, X_2,X_3,X_4)$ | |
|---|---|---|
| 所有元素 | 平面上的所有直线 | {+1,+1,+1,+1}, {+1,+1,+1,-1}… |
| 元素个数 | $\infty$ | 最大为14 (不会超过 $2^N$) |
我们知道, $\mathcal{H}(X_1, X_2,…,X_N)$ 的元素个数(即 $|\mathcal{H}(X_1, X_2,…,X_N)|$ )是取决于具体的数据集 $\mathcal{D}$ 的,例如当 $N=3$ 时且三个点不在一条直线时对分数为8,而在一条直线时对分数是6。为了去掉对具体 $\mathcal{D}$ 的依赖性,我们引入 增长函数(growth function):
假设空间 $\mathcal{H}$ 的增长函数 $m_{\mathcal{H}}(N)$ 为
$$
m_{\mathcal{H}}(N) = \underset{X_1,X2,…,X_N \in \mathcal{X}}{max} |\mathcal{H}(X_1, X_2,…,X_N)|
$$
增长函数 $m_{\mathcal{H}}(N)$ 表示假设空间 $\mathcal{H}$ 对个任意 $N$ 个样本所能赋予标记的的最大可能结果数,其上界为 $2^N$ 。
显然,$m_{\mathcal{H}}(N)$ 越大,$\mathcal{H}$ 的表示能力越强。因此,增长函数描述了假设空间 $\mathcal{H}$ 的表示能力,由此反映出假设空间的复杂度。既然如此,那我们可不可以用 $m_{\mathcal{H}}(N)$ 直接替换掉式$(2.1.2)$ 中的 $\text{effective}(M)$ 呢,即
$$
\forall g \in \mathcal{H}, \mathbb{P}[|E_{in}(g) - E_{out}(g)| > \epsilon] \overset{?}{\leq} 2 m_{\mathcal{H}}(N) \exp(-2 \epsilon^2 N) \tag{2.2.1}
$$
我们将在在2.3节回答这个问题。
2.3 VC界
2.3.1 打散(shatter)
在介绍VC维界(VC bound)之前,先引入打散(shatter)的概念,
当假设空间 $\mathcal{H}$ 作用于大小为 $N$ 的样本集 $\mathcal{D}$ 时,产生的对分数量等于 $2^N$ 即 $m_{\mathcal{H}}(N)=2^N$ 时,就称 $\mathcal{D}$ 被 $\mathcal{H}$ 打散了。
shatter的原意是打碎,在此指 $N$ 个点的所有(碎片般的)可能情形都被 $\mathcal{H}$ 产生了。
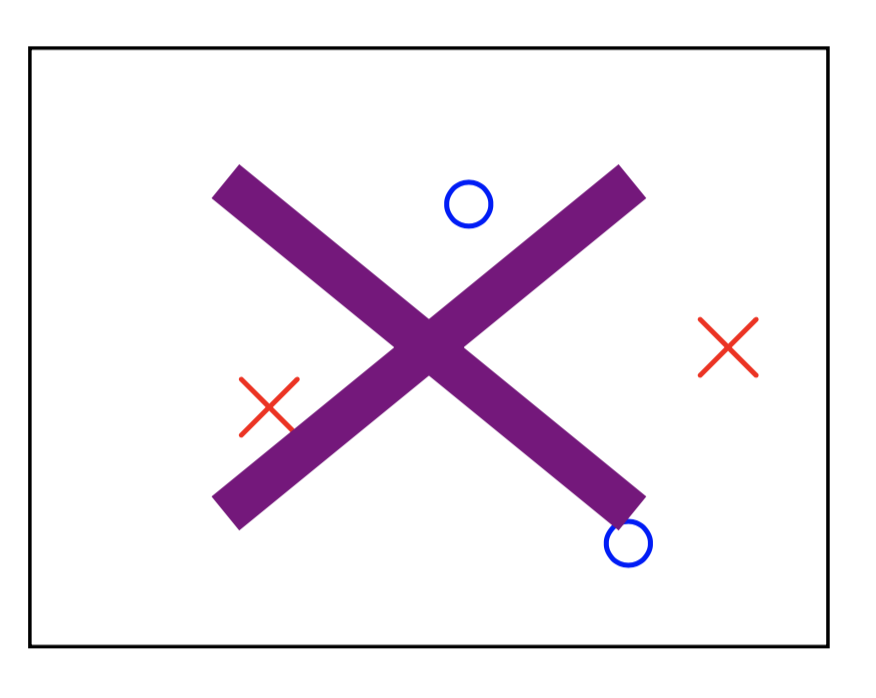
如上图所示,二维空间上的的三个点(不在一条直线上)可以被平面上所有直线这个假设空间打碎,此时 $m_{\mathcal{H}}(3)= 8 = 2^3$。但如下图所示的四个点就不能被这个假设空间打碎了,可知此时 $m_{\mathcal{H}}(4)=14 \neq 2^4$。
2.3.2 break point
尽管增长函数把假设数从无穷缩小到 $2^N$,但是这个量级还是太大了,很难保证式$(1.3.3)$右边这个上界趋于0,所以能不能把量级再缩小一点?
为了回答这个问题,先给出break point的定义:
对于假设空间 $\mathcal{H}$ 的增长函数 $m_{\mathcal{H}}(N)$ ,从 $N=1$ 出发逐渐增大,当增大到 $k$ 时,出现 $m_{\mathcal{H}}(N) < 2^N$ 的情形,则我们说 $k$ 是该假设空间的break point。换句话说,对于任何大小为 $N(N \ge k)$ 的数据集, $\mathcal{H}$ 都没有办法打碎它。
举例来讲,由2.3.1节知,当假设空间 $\mathcal{H}$ 定义为平面上所有直线时,其break point就为4。
有了break point的概念,再经过一系列归纳证明(详见台大机器学习课程lecture6),我们有这样一个结论:
设break point存在且为 $k$ 的假设空间的增长函数上界为 $B(N,k)$,则 $B(N,k)$ 满足
$$
m_{\mathcal{H}}(N) \le B(N,k) \le \sum_{i=0}^{k-1}{N \choose i} \le N^{k-1}
$$
注: 上式的证明可见这个知乎回答,另外最后一个不等号仅在 $N \ge 2$ 且 $k \ge 2$ 时成立。
即break point存在时增长函数上界是一个多项式,多项式的最高幂次项为 $N^{k–1}$。
所以我们得到结论:如果break point存在,则增长函数 $m_{\mathcal{H}}(N)$ 是多项式的。多项式的量级就比 $2^N$ 小多了,这就很容易保证式$(1.3.3)$右边这个上界很小,学习就可行了!
2.3.3 VC界
上一小节提到如果break point存在,学习是可行的。既然如此,我们来回答一下2.2节最后提出的问题: 可不可以用 $m_{\mathcal{H}}(N)$ 直接替换掉式$(2.1.2)$ 中的 $\text{effective}(M)$ 呢,即式$(2.2.1)$是否成立。
答案是不能直接替换,正确的不等式是
$$
\forall g \in \mathcal{H}, \mathbb{P}[|E_{in}(g) - E_{out}(g)| > \epsilon] \leq 4 m_{\mathcal{H}}(2N) \exp(-\frac18 \epsilon^2 N) \tag{2.3.1}
$$
上式其实和式 $(2.2.1)$ 差不多,其证明略显复杂我们暂不去探究,可参考此处。
式$(2.3.1)$就是VC界,这个公式的意义在于:如果假设空间 $\mathcal{H}$ 存在有限的break point $k$,即 $m_{\mathcal{H}}(2N)$ 会被最高幂次为 $k–1$ 的多项式上界给约束住,那么,随着 $N$ 的逐渐增大,指数式 $exp(\cdot)$ 的下降会比多项式 $m_{\mathcal{H}}(2N)$ 的增长速度更快,所以此时可以推断出VC界是有界的。更进一步,当 $N$ 足够大时,对于 $\mathcal{H}$ 中的任意一个假设 $g$ ,$E_{in}(g)$ 都将接近于 $E_{out}(g)$,即学习是可行的。
2.4 VC维
现在,我们终于可以定义VC维了:
假设空间 $\mathcal{H}$ 的VC维是能被 $\mathcal{H}$ 打散的最大数据集的大小,即
$$
VC(\mathcal{H}) = max \lbrace N: m_{\mathcal{H}}(N) = 2^N\rbrace
$$
根据此定义,有 $VC(\mathcal{H}) = k-1$,其中 $k$ 是 $\mathcal{H}$ 的break point。
$VC(\mathcal{H}) = d$ 表明存在大小为 $d$ 的数据集能被假设空间 $\mathcal{H}$ 打散,需要注意的是这并不意味着所有大小为 $d$ 的数据集都能被 $\mathcal{H}$ 打散,例如二维平面上的所有直线构成的假设空间 $\mathcal{H}$ 的VC维为3,但是它并不能打散位于同一条直线上的三个点。事实上,VC维的定义与数据具体分布是无关的。
因为 $VC(\mathcal{H}) = k-1$,所以由2.3.2节可知当 $N \ge 2$ 且 $k \ge 2$ 时,有
$$
m_{\mathcal{H}}(N) \le N^{VC(\mathcal{H})} \tag{2.4.1}
$$
将上式代入$(2.3.1)$的右边VC界有
$$
\forall g \in \mathcal{H}, \mathbb{P}[|E_{in}(g) - E_{out}(g)| > \epsilon] \leq 4 (2N)^{VC(\mathcal{H})} \exp(-\frac18 \epsilon^2 N) \tag{2.4.2}
$$
所以,1.3节的可学习的两个核心条件等价于:
- 学习算法 $\mathcal{A}$ 能够从 $\mathcal{H}$ 选出的假设 $g$ 满足 $E_{in}(g) \approx 0$。再结合条件2即达到了 $E_{out}(g) \approx 0$ 的目标。
- 假设空间 $\mathcal{H}$ 的VC维 $VC(\mathcal{H})$ 是有限的且训练样本数 $N$ 足够大。此时可保证式(2.4.2)右边上界趋于0,即学习算法 $\mathcal{A}$ 从 $\mathcal{H}$ 选出的任意假设 $g$ 都满足 $E_{in}(g) \approx E_{out}(g)$。
VC维反映了函数集的学习能力,VC维越大,能学到的模型越复杂。根据前面的推导,我们知道VC维的大小与学习算法无关,与数据集的具体分布无关,与我们求解的目标函数也无关,只与模型和假设空间有关。另外,实践中有这样一个规律:一般情况下,假设空间的VC维约等于假设自由变量的数目。
2.5 $E_{in}(g)$ 与 $E_{out}(g)$ 的关系
令式$(2.4.2)$右边的 $4 (2N)^{VC(\mathcal{H})} \exp(-\frac18 \epsilon^2 N) = \delta$,即坏事发生的概率
$$
\mathbb{P}[|E_{in}(g) - E_{out}(g)| > \epsilon] \leq \delta \tag{2.5.1}
$$
则可反解出
$$
\epsilon = \sqrt{\frac 8 N \ln \left( \frac {4(2N)^{VC(\mathcal{H})}} \delta \right)} \tag{2.5.2}
$$
由(2.5.1)可得出,有 $1-\delta$ 的概率好事情会发生,好事情即
$$
E_{in}(g) - \sqrt{\frac 8 N \ln \left( \frac {4(2N)^{VC(\mathcal{H})}} \delta \right)} \le E_{out}(g) \le E_{in}(g) + \sqrt{\frac 8 N \ln \left( \frac {4(2N)^{VC(\mathcal{H})}} \delta \right)} \tag{2.5.3}
$$
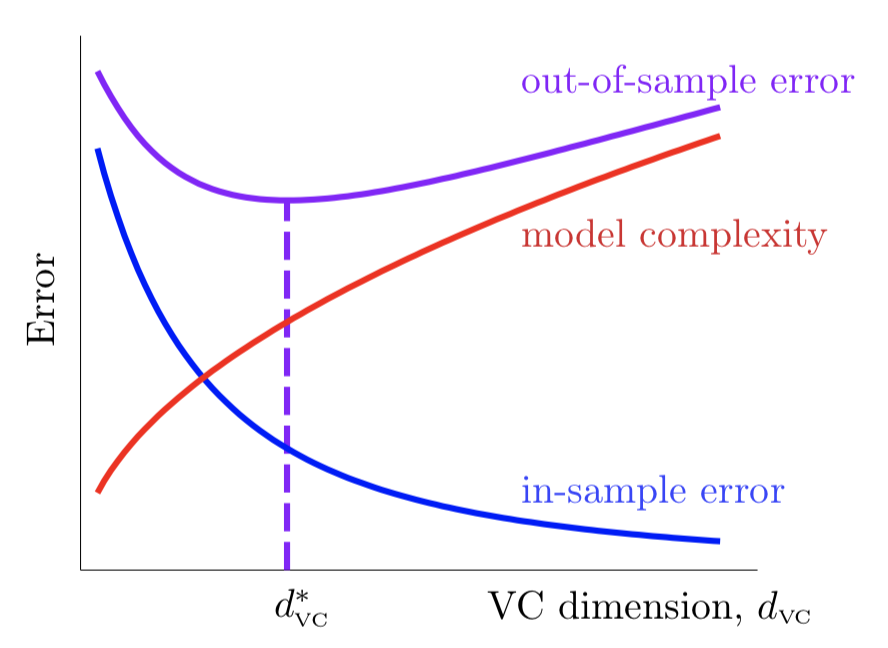
上式就是 $E_{in}(g)$ 与 $E_{out}(g)$ 的关系。其中,根号部分也可以看做模型的复杂度 $\Omega$,模型越复杂,$E_{in}(g)$ 与 $E_{out}(g)$ 离得越远。如图2.5所示,当固定样本数 $N$ 时,随着VC维的上升,$E_{in}(g)$ 会不断降低,而复杂度 $\Omega$ 会不断上升,其上升与下降的速度在每个阶段都有所不同,因此我们要寻找一个二者兼顾的比较合适的VC维使 $E_{out}(g)$ 最小。
此外,由上面的分析易知,样本数 $N$ 也会影响 $E_{out}(g)$。例如,当前有一个 $VC(\mathcal{H})=3$ 的假设空间,要使 $\epsilon=0.1$ 且 $\delta=0.1$,则要想满足式$(2.5.2)$,可计算出理论上样本数 $N$ 需要达到 $10000VC(\mathcal{H})$ 这个量级,但实际应用中我们发现 $N$ 达到 $10VC(\mathcal{H})$ 就够了。这是因为,VC界是一个及其宽松的上界,因为它需要对任何学习算法,对任何数据分布,对任何目标函数都要成立,所以实际应用中的上界要比VC界小很多。
3. 总结
总结一下本文的行文思路,
- 先用Hoeffding不等式说明了可学习的两个条件:
(1) 学习算法 $\mathcal{A}$ 能够从 $\mathcal{H}$ 选出的假设 $g$ 满足 $E_{in}(g) \approx 0$。
(2) 假设空间 $\mathcal{H}$ 中假设数 $M$ 是有限的且训练样本数 $N$ 足够大。 - 但假设空间 $\mathcal{H}$ 中假设数 $M$ 往往是无穷大的。幸运的是,在推导出条件(2)时,我们要求假设空间的所有假设都是独立的,而假设空间 $\mathcal{H}$ 中独立假设数 $\text{effective}(M)$ 却是有限的,增长函数告诉我们 $\text{effective}(M)$ 的上界为 $2^N$ 。
- $2^N$ 这个上界还是太大了,学习还是很难可行。所以我们又引入了break point的概念,使 $2^N$ 的量级降为 $N^{k-1}$, 由此得到了VC界。
- 然后我们给出了VC维的定义,可学习的两个条件转变为:
(1) 学习算法 $\mathcal{A}$ 能够从 $\mathcal{H}$ 选出的假设 $g$ 满足 $E_{in}(g) \approx 0$。
(2) 假设空间 $\mathcal{H}$ 的VC维 $VC(\mathcal{H})$ 是有限的且训练样本数 $N$ 足够大。 - 最后我们讨论了 $E_{in}(g)$ 与 $E_{out}(g)$ 的关系,发现为了使学习器更好($E_{out}(g)$更小),要选择合适的VC维,不能太大也不能太小。
因笔者自身水平实在有限,如果文章有任何的不妥,还请读者告之。此外,VC维可以说是机器学习中的一大核心,并非一篇博客就可以讲解透彻,所以本文也省略了一些复杂的证明,如果想深入理解可以去查阅相关书籍或论文。

