目前网上大多数博客只介绍了AdaBoost算法是什么,但是鲜有人介绍为什么Adaboost长这样,本文对此给出了详细的解释。
1. 概述
1.1 集成学习
目前存在各种各样的机器学习算法,例如SVM、决策树、感知机等等。但是实际应用中,或者说在打比赛时,成绩较好的队伍几乎都用了集成学习(ensemble learning)的方法。集成学习的思想,简单来讲,就是“三个臭皮匠顶个诸葛亮”。集成学习通过结合多个学习器(例如同种算法但是参数不同,或者不同算法),一般会获得比任意单个学习器都要好的性能,尤其是在这些学习器都是”弱学习器”的时候提升效果会很明显。
弱学习器指的是性能不太好的学习器,比如一个准确率略微超过50%的二分类器。
下面看看西瓜书对此做的一个简单理论分析。
考虑一个二分类问题 $y \in {-1, +1}$ 、真实函数 $f$ 以及奇数 $M$ 个犯错概率相互独立且均为 $\epsilon $ 的个体学习器(或者称基学习器) $h_i$ 。我们用简单的投票进行集成学习,即分类结果取半数以上的基学习器的结果:
$$
H(x) = sign(\sum_{i=1}^M h_i(x)) \tag{1.1.1}
$$
由Hoeffding不等式知,集成学习后的犯错(即过半数基学习器犯错)概率满足
$$
P(H(x) \neq f(x)) \leq exp(- \frac 1 2 M (1-2\epsilon)^2) \tag{1.1.2}
$$
式 $(1.1.2)$ 的证明是周志华《机器学习》的习题8.1,题解可参考此处
式 $(1.1.2)$ 指出,当犯错概率独立的基学习器个数 $M$ 很大时,集成后的犯错概率接近0,这也很符合直观想法: 大多数人同时犯错的概率是比较低的。
就如上面加粗字体强调的,以上推论全部建立在基学习器犯错相互独立的情况下,但实际中这些学习器不可能相互独立,而如何让基学习器变得“相对独立一些”,也即增加这些基学习器的多样性,正是集成学习需要考虑的主要问题。
按照每个基学习器之间是否存在依赖关系可以将集成学习分为两类:
- 基学习器之间存在强依赖关系,一系列基学习器需要串行生成,代表算法是Boosting;
- 基学习器之间不存在强依赖关系,一系列基学习器可并行生成,代表算法是Bagging和随机森林。
Boosting系列算法里最著名算法主要有AdaBoost和提升树(Boosting tree)系列算法,本文只介绍最具代表性的AdaBoost。提升树、Bagging以及随机森林不在本文介绍范围内,有时间了再另外介绍。
1.2 Boosting
Boosting指的是一类集成方法,其主要思想就是将弱的基学习器提升(boost)为强学习器。具体步骤如下:
- 先用每个样本权重相等的训练集训练一个初始的基学习器;
- 根据上轮得到的学习器对训练集的预测表现情况调整训练集中的样本权重(例如提高被错分类的样本的权重使之在下轮训练中得到更多的关注), 然后据此训练一个新的基学习器;
- 重复2直到得到 $M$ 个基学习器,最终的集成结果是 $M$ 个基学习器的组合。
由此看出,Boosting算法是一个串行的过程。
Boosting算法簇中最著名的就是AdaBoost,下文将会详细介绍。
2. AdaBoost原理
2.1 基本思想
对于1.2节所述的Boosting算法步骤,需要回答两个问题:
- 如何调整每一轮的训练集中的样本权重?
- 如何将得到的 $M$ 个组合成最终的学习器?
AdaBoost(Adaptive Boosting, 自适应增强)算法采取的方法是:
- 提高上一轮被错误分类的样本的权值,降低被正确分类的样本的权值;
- 线性加权求和。误差率小的基学习器拥有较大的权值,误差率大的基学习器拥有较小的权值。
Adaboost算法结构如下图(图片来源)所示。
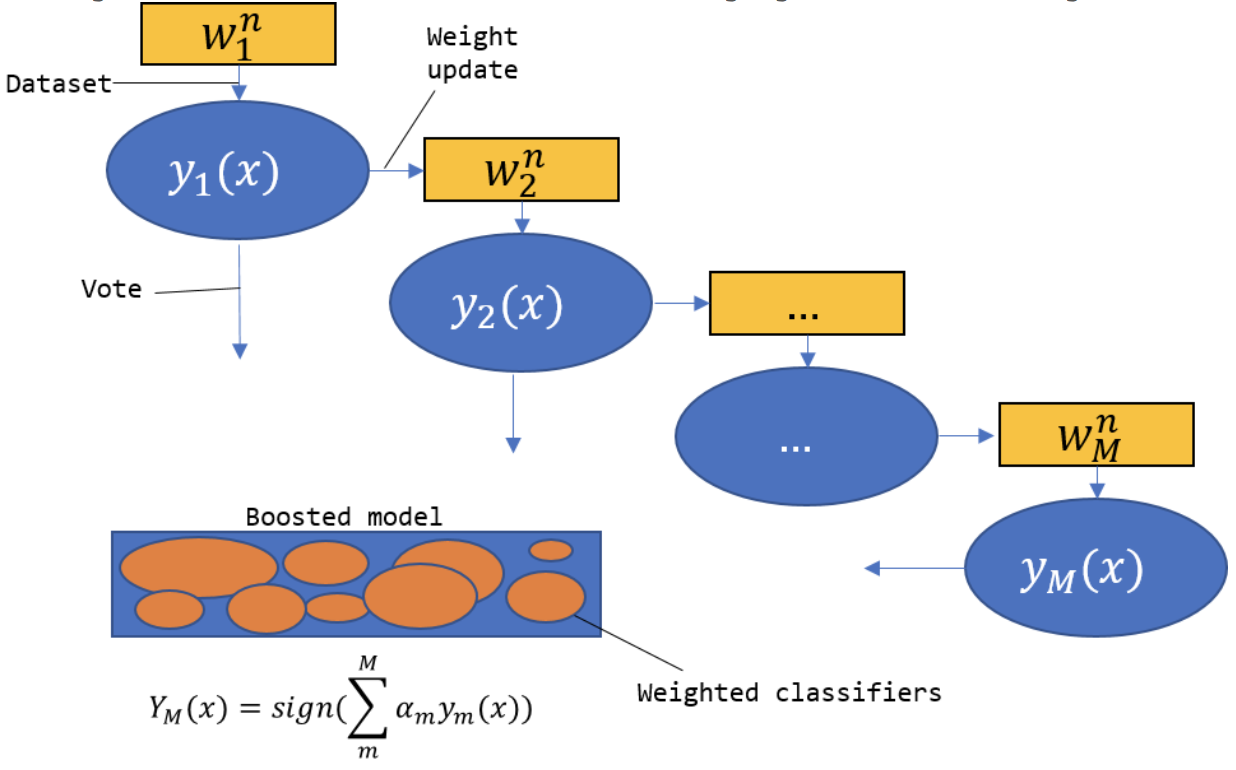
下面先给出AdaBoost算法具体实现步骤,至于算法解释(为什么要这样做)将在下一大节阐述。
2.2 算法步骤
考虑如下形式的二分类(标准AdaBoost算法只适用于二分类任务)训练数据集:
$$
{(x_1,y_1),(x_2,y_2),…,(x_N,y_N)}
$$
其中 $x_i$是一个含有$d$个元素的列向量, 即 $x_i\in \mathcal{X} \subseteq \mathbf{R}^d$ ; $y_i$是标量, $y\in{+1,-1}$。
Adaboost算法具体步骤如下:
- 初始化样本的权重
$$
D_1=(w_{11}, w_{12},…w_{1N}), w_{1i}=\frac 1 N, i = 1,2…N \tag{2.2.1}
$$ - 对$m = 1,2,…M$,重复以下操作得到 $M$ 个基学习器:
(1) 按照样本权重分布 $D_m$ 训练数据得到第 $m$ 个基学习器 $G_m(x)$:
$$
G_m(x): \mathcal{X} \to {-1, +1}
$$
(2) 计算 $G_m(x)$ 在加权训练数据集上的分类误差率:
$$
e_m = \sum_{i=1}^NP(G_m(x_i) \neq y_i)=\sum_{i=1}^N w_{mi} I(G_m(x_i) \neq y_i) \tag{2.2.2}
$$
上式中 $I(\cdot)$ 是指示函数,考虑更加周全的AdaBoost算法在这一步还应该判断是否满足基本条件(例如生成的基学习器是否比随机猜测好), 如果不满足,则当前基学习器被抛弃,学习过程提前终止。
(3) 计算 $G_m(x)$ 的系数(即最终集成使用的的基学习器的权重):
$$
\alpha_m = \frac 1 2 log \frac {1-e_m} {e_m} \tag{2.2.3}
$$
(4) 更新训练样本的权重
$$
D_{m+1}=(w_{m+1,1}, w_{m+1,2},…w_{m+1,N}) \tag{2.2.4}
$$
$$
w_{m+1, i} = \frac{w_{mi}} {Z_m} exp(-\alpha_my_iG_m(x_i)) ,i=1,2,…N \tag{2.2.5}
$$
其中 $Z_m$ 是规范化因子,目的是为了使 $D_{m+1}$ 的所有元素和为1。即
$$
Z_m=\sum_{i=1}^N w_{mi} exp(-\alpha_my_iG_m(x_i)) \tag{2.2.6}
$$ - 构建最终的分类器线性组合
$$
f(x) = \sum_{i=1}^M \alpha_m G_m(x) \tag{2.2.7}
$$
得到最终的分类器为
$$
G(x) = sign(f(x))=sign(\sum_{i=1}^M \alpha_m G_m(x)) \tag{2.2.8}
$$
由式 $(2.2.3)$ 知,当基学习器 $G_m(x)$ 的误差率 $e_m \le 0.5$ 时,$\alpha_m \ge 0$,并且 $\alpha_m$ 随着 $e_m$ 的减小而增大,即分类误差率越小的基学习器在最终集成时占比也越大。即AdaBoost能够适应各个弱分类器的训练误差率,这也是它的名称中”适应性(Adaptive)”的由来。
由式 $(2.2.5)$ 知, 被基学习器 $G_m(x)$ 误分类的样本权值得以扩大,而被正确分类的样本的权值被得以缩小。
需要注意的是式 $(2.2.7)$ 中所有的 $\alpha_m$ 的和并不为1(因为没有做一个softmax操作),$f(x)$ 的符号决定了所预测的类,其绝对值代表了分类的确信度。
3. AdaBoost算法解释
有没有想过为什么AdaBoost算法长上面这个样子,例如为什么 $\alpha_m$ 要用式 $(2.2.3)$ 那样计算?本节将探讨这个问题。
3.1 前向分步算法
在解释AdaBoost算法之前,先来看看前向分步算法。
就以AdaBoost算法的最终模型表达式为例:
$$
f(x) = \sum_{i=1}^M \alpha_m G_m(x) \tag{3.1.1}
$$
可以看到这是一个“加性模型(additive model)”。我们希望这个模型在训练集上的经验误差最小,即
$$
min \sum_{i=1}^N L(y_i, f(x)) \iff min \sum_{i=1}^N L(y_i, \sum_{i=1}^M \alpha_m G_m(x)) \tag{3.1.2}
$$
通常这是一个复杂的优化问题。前向分步算法求解这一优化问题的思想就是: 因为最终模型是一个加性模型,如果能从前往后,每一步只学习一个基学习器 $G_m(x)$ 及其权重 $\alpha_m$ , 不断迭代得到最终的模型,那么就可以简化问题复杂度。具体的,当我们经过 $m-1$ 轮迭代得到了最优模型 $f_{m-1}(x)$ 时,因为
$$
f_m(x)= f_{m-1}(x) + \alpha_mG_m(x) \tag{3.1.3}
$$
所以此轮优化目标就为
$$
min \sum_{i=1}^N L(y_i, f_{m-1}(x) + \alpha_mG_m(x)) \tag{3.1.4}
$$
求解上式即可得到第 $m$ 个基分类器 $G_m(x)$ 及其权重 $\alpha_m$ 。
这样,前向分步算法就通过不断迭代求得了从 $m=1$ 到 $m=M$ 的所有基分类器及其权重,问题得到了解决。
3.2 AdaBoost算法证明
上一小结介绍的前向分步算法逐一学习基学习器,这一过程也即AdaBoost算法逐一学习基学习器的过程。但是为什么2.2节中的公式为什么长那样还是没有解释。本节就证明前向分步算法的损失函数是指数损失函数(exponential loss function)时,AdaBoost学习的具体步骤就如2.2节所示。
指数损失函数即
$$
L(y, f(x)) = exp(-yf(x))
$$
周志华《机器学习》p174有证明,指数损失函数是分类任务原本0/1损失函数的一致(consistent)替代损失函数,由于指数损失函数有更好的数学性质,例如处处可微,所以我们用它替代0/1损失作为优化目标。
将指数损失函数代入式 $(3.1.4)$ ,优化目标就为
$$
\underset{\alpha_m,G_m}{argmin} \sum_{i=1}^N exp[-y_i(f_{m-1}(x) + \alpha_mG_m(x))] \tag{3.2.1}
$$
因为 $y_if_{m-1}(x)$ 与优化变量 $\alpha$ 和 $G$ 无关,如果令
$$
w_{m,i} = exp[-y_i f_{m-1}(x)] \tag{3.2.2}
$$
这个 $w_{m,i}$ 其实就是2.2节中归一化之前的权重 $w_{m,i}$
那么式 $(3.2.1)$ 等价于
$$
\underset{\alpha_m,G_m}{argmin} \sum_{i=1}^N w_{m,i}exp(-y_i\alpha_mG_m(x)) \tag{3.2.3}
$$
我们分两步来求解式 $(3.2.3)$ 所示的优化问题的最优解 $\hat{\alpha}_m$ 和 $\hat{G}_m(x)$ :
对任意的 $\alpha_m > 0$, 求 $\hat{G}_m(x)$:
$$
\hat{G}_m (x) = \underset{G_m}{argmin} \sum_{i=1}^N w_{m,i} I(y_i \neq G_m(x_i)) \tag{3.2.4}
$$上式将指数函数换成指示函数是因为前面说的指数损失函数和0/1损失函数是一致等价的。
式子 $(3.2.4)$ 所示的优化问题其实就是AdaBoost算法的基学习器的学习过程,即2.2节的步骤2(1),得到的 $\hat{G}_m(x)$ 是使第 $m$ 轮加权训练数据分类误差最小的基分类器。
求解 $\hat{\alpha}_m$ :
将式子 $(3.2.3)$ 中的目标函数展开
$$
\begin{aligned}
\sum_{i=1}^N w_{m,i}exp(-y_i\alpha_mG_m(x)) &= \sum_{y_i=G_m(x_i)} w_{m,i}e^{- \alpha} + \sum_{y_i \neq G_m(x_i)}w_{m,i}e^{\alpha} \\\\
& = (e^{\alpha} - e^{-\alpha}) \sum_{i=1}^N w_{m,i} I(y_i \neq G_m(x_i)) + e^{-\alpha} \sum_{i=1}^N w_{m,i}
\end{aligned} \tag{3.2.5}
$$注:为了简洁,上式子中的$\hat{G}_m(x)$ 被略去了 $\hat{\cdot}$ , $\alpha_m$ 被略去了下标 $m$ ,下同
将上式对 $\alpha$ 求导并令导数为0,即
$$
(e^{\alpha} + e^{-\alpha}) \sum_{i=1}^N w_{m,i} I(y_i \neq G_m(x_i)) - e^{-\alpha} \sum_{i=1}^N w_{m,i} = 0 \tag{3.2.6}
$$
解得
$$
\hat{\alpha}_m = \frac 1 2 log \frac {1-e_m} {e_m} \tag{3.2.7}
$$
其中, $e_m$ 是分类误差率:
$$
e_m = \frac {\sum_{i=1}^N w_{m,i} I(y_i \neq G_m(x_i)} {\sum_{i=1}^N w_{mi}} \tag{3.2.8}
$$
如果式子 $(3.2.8)$ 中的 $w_{mi}$ 归一化成和为1的话那么式 $(3.2.8)$ 也就和2.2节式 $(2.2.2)$ 一模一样了,进一步地也有上面的 $\hat{\alpha}_m$ 也就是2.2节的 $\alpha_m$ 。
最后来看看每一轮样本权值的更新,由 $(3.1.3)$ 和 $(3.2.2)$ 可得
$$
w_{m+1,i} = w_{m,i} exp[-y_i \alpha_m G_{m}(x)] \tag{3.2.9}
$$
如果将上式进行归一化成和为1的话就和与2.2节中 $(2.2.5)$ 完全相同了。
由此可见,2.2节所述的AdaBoost算法步骤是可以经过严密推导得来的。总结一下,本节推导有如下关键点:
- AdaBoost算法是一个加性模型,将其简化成前向分步算法求解;
- 将0/1损失函数用数学性质更好的指数损失函数替代。
4. python实现
4.1 基学习器
首先需要定义一个基学习器,它应该是一个弱分类器。
弱分类器使用库 sklearn 中的决策树分类器DecisionTreeClassifier, 可设置该决策树的最大深度为1。1
2# Fit a simple decision tree(weak classifier) first
clf_tree = DecisionTreeClassifier(max_depth = 1, random_state = 1)
4.2 AdaBoost实现
然后就是完整AdaBoost算法的实现了,如下所示。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37def my_adaboost_clf(Y_train, X_train, Y_test, X_test, M=20, weak_clf=DecisionTreeClassifier(max_depth = 1)):
n_train, n_test = len(X_train), len(X_test)
# Initialize weights
w = np.ones(n_train) / n_train
pred_train, pred_test = [np.zeros(n_train), np.zeros(n_test)]
for i in range(M):
# Fit a classifier with the specific weights
weak_clf.fit(X_train, Y_train, sample_weight = w)
pred_train_i = weak_clf.predict(X_train)
pred_test_i = weak_clf.predict(X_test)
# Indicator function
miss = [int(x) for x in (pred_train_i != Y_train)]
print("weak_clf_%02d train acc: %.4f"
% (i + 1, 1 - sum(miss) / n_train))
# Error
err_m = np.dot(w, miss)
# Alpha
alpha_m = 0.5 * np.log((1 - err_m) / float(err_m))
# New weights
miss2 = [x if x==1 else -1 for x in miss] # -1 * y_i * G(x_i): 1 / -1
w = np.multiply(w, np.exp([float(x) * alpha_m for x in miss2]))
w = w / sum(w)
# Add to prediction
pred_train_i = [1 if x == 1 else -1 for x in pred_train_i]
pred_test_i = [1 if x == 1 else -1 for x in pred_test_i]
pred_train = pred_train + np.multiply(alpha_m, pred_train_i)
pred_test = pred_test + np.multiply(alpha_m, pred_test_i)
pred_train = (pred_train > 0) * 1
pred_test = (pred_test > 0) * 1
print("My AdaBoost clf train accuracy: %.4f" % (sum(pred_train == Y_train) / n_train))
print("My AdaBoost clf test accuracy: %.4f" % (sum(pred_test == Y_test) / n_test))

